The Origin of the European Folk Music Scale: A New Theory

Over a century ago, musicians noticed that European folk music seemed to exhibit certain uniform traits. They tried to analyse the music based upon the vast musical knowledge that they believed they had. The result was that folk music was described as tetratonic (four notes per octave), pentatonic (five notes per octave), or hexatonic (six notes per octave) because the music seemed to be “gapped” in some way. Musicologists also applied the ecclesiastical modal naming scheme,^[i] which is a bit odd since that modal naming convention requires seven notes per octave, and the modes are defined by the precise placement of two half-steps; yet, European folk music is missing one (hexatonic) or both (tetratonic and pentatonic) half steps. All of these terms and approaches originate from the frame of reference of the diatonic scale, which demonstrates the characteristic of octave equivalency; that is, there are an equal number of notes per octave. If the terms used by musicologists to describe folk music don’t seem to be successful, could it be that the folk music scale is based on a non-diatonic scale? If so, how can we conjure up a solution from the undocumented musical tradition of more than a millennium ago to solve the problem?

I have attempted to answer this question by looking at the material culture available at that time. Music was mainly sung^.[ii] Instruments were extremely rare.^[iii] What instruments that did exist were those that assisted in the accomplishment of work. If you examine marginalized societies today where there are still shepherds working in relative isolation in the Carpathians (Russia/Ukraine), Poland, the Balkans, Estonia, Romania, Sweden, Norway, etc., you will still see them carrying an instrumental tool. It was made by taking a branch or the trunk of a small tree, splitting it, hollowing it out, putting the two halves back together secured with sap and birch-bark or osier (willow) rings. It was a wooden, valve-less, finger-hole-less trumpet; in short, it was a wooden shepherd’s trumpet. These shepherds’ trumpets had various names such as trambita, trâmbiţa, trembita (tрембіта), trombita, tulnic, trimitis, taures, torvi, touhitorvi, näverlur, neverlur, alphorn, vallehorn, karjapasun, bucium (from which we have in English “bugle”), etc. Such names are obvious cognates to modern forms such as trompeta (Spanish), tromba (Italian), trompette (French), trompete (German), “trumpet” and the earlier “trump” (English). These trumpets played the harmonic or overtone series (I prefer the term natural scale); most people are familiar with this from hearing bugle calls such as “Taps” and “Reveille.” 

So, what is the natural scale? When you pluck a string or buzz your lips on a tube, the resulting sound is actually a series of notes played at once. You’re hearing the frequency produced by the movement of, say, the whole length of a string on a violin displacing air when plucked. Yet the string is flexible, and there can be two, three, four, or more waves that can fit along the length of the string; those waves produce pitches as well. They are very faint on a stringed instrument, but on a wind instrument, you can blow harder to make one overtone louder than another and clearly hear it (that overtone is all that you hear, really). Here are the pitches that can be produced on an 8’ long shepherd’s trumpet (Figure 1, below). A “partial” is the number of whole waves that that fit within its tube.

Figure 1: The Natural Scale as it is Often Presented

The first thing that stands out is that the notes are gapped at the lower end (left side) and become closer together as the pitches ascend (to the right). The black notes are pitches that are very much different in intonation from the diatonic scale; arrows point in the direction the pitch sounds in relation to the equally tempered scale. The first partial is nearly impossible to play as are C₂ and C₃; however, G₃, is attainable. After that, the lower pitches are much easier to play than the higher pitches, C₄ perhaps being the easiest.

Imagine a transcriber in the past listening to a tune played on a shepherd’s trumpet. Envision a trumpeter playing the 7^th partial and ending the tune end on C; the transcriber would not consider the pitch of B♭₄ for the 7^th partial since B♭₄ is not in the key of C major. The choice would be between A₄ and B♮₄. Since the 7^th partial is closer to A₄, the transcriber would probably write A₄ when it’s heard. Also, in the figure above, the 11^th partial is written as F♯₅; it could also be written as F♮₅ since it is almost exactly halfway between the two notes. Again, given the choice, a transcriber would probably write F♮5 since F♯₅ is not in the key of C major. The other possibility is to write F♯₅ if the tune ended in G (or E), but this condition is easy to identify.

If the natural scale’s representation on the diatonic staff is adjusted with these concerns in mind, the playable notes might be represented as this (Figure 2, below):

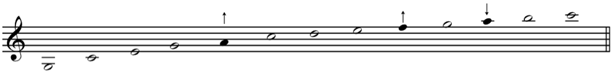
Figure 2: The Natural Scale as Transcribers May Have Used It

It should be pointed out that although the natural scale looks unevenly placed on the figure above, it is in fact linear with respect to frequency; if available notes are plotted against those notes’ frequencies, the following results (see Figure 3, below):

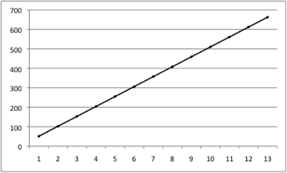
Figure 3: The Natural Scale; Notes Available vs. Frequency (Cycles per Second)

The x-axis is the note value (here the partial number, but it is just the integer value of the notes available, in order); the corresponding frequency value in Hertz (cycles-per-second) is placed on the y-axis. The diatonic scale is much different. In the chart below, I have placed the notes of the diatonic scale in order as integer values and plotted that against the frequency of the pitches beginning on C₄ (C₄, D₄, E₄, F₄, G₄, A₄, etc.; see Figure 4, below):

Figure 4: The Diatonic Equally Tempered Scale; Note Number vs. Frequency

Here the x-axis reflects the note value (1=C, 2=D, 3=E, etc.); the corresponding frequency is placed on the y-axis. I deliberately placed the notes equidistantly on the x-axis in order to highlight the uneven nature of the diatonic scale. If I had placed the half steps halfway between the whole steps, you would see that the points trace a smooth parabolic curve (in equal temperament), not a straight line.

A comparison of Figure 3 and Figure 4 evidence that the diatonic scale and the natural scale are vastly different. One is exponential with respect to frequency (diatonic), the other linear (natural). If you make the diatonic scale linear in your mind (as most people do), then the natural scale appears to be logarithmic, as in Figure 2. Attempting to transcribe tunes played on instruments using the natural scale with the diatonic scale notational system is like trying to fit a square peg in a round hole: it just doesn’t work.

Consider Figure 2 again. If a trained musician hears a shepherd’s trumpet playing in the lower range (G₃, C₄, E₄, G₄, A₄, C₅), the musician will classify the tune as tetratonic (four notes per octave; that is, four notes ascending including and starting on C₄, and then the octave, C₅). If the tune happens to rise to D₅, the diatonically, octave-equivalent trained musician will then assume that D₄ is in existence and declare that the tune is pentatonic (missing F₄ and B₄, but having five notes per octave); the pitches assumed to be present are G₃, C₄, (D₄), E₄, G₄, A₄, C₅, D₅, etc., when in fact D₄ does not appear in the tune at all. A similar erroneous assumption may occur again on a different note (11^th partial, F₅) as a shepherd’s trumpet ascends in pitch. A tune that would be classified as pentatonic (missing all Fs and Bs) would be declared hexatonic once F₅ is found, because the lower octave F₄ is assumed to be in existence (having C₄, (D₄), E₄, (F₄), G₄, A₄, C₅, D₅, E₅, F₅, etc.). This classification occurs even though both D₄ and F₄ do not in fact exist.^[iv]

Simply put, because diatonically trained musicians think in terms of seven notes per octave or “octave equivalency,” it has never occurred to them that they were dealing with a system that was not octave-based. This is understandable since the two systems have become linked and intertwined today.

If my theory is true, then it becomes clear why the ecclesiastical modes were used to describe folk music;^[v] it also explains the percentages with which each individual mode is alleged to have occurred. If a tune played on a shepherd’s trumpet ends on the 3^rd, 4^th, 5^th, etc. partial, transcribers would suggest that the tune would be, in order: G major (3^rd partial; I have never seen this occur and will ignore this possibility), C major (4^th partial), E minor (5^th partial, as the relative minor to G major with the 11^th partial heard as F♯₅), G major or G mixolydian (6^th partial), A minor (7^th partial, as the relative minor to C major), C major (8^th partial), D dorian (9^th partial), E phrygian (10^th partial), etc., from easiest to play to more difficult to play (which is a reflection of airstream flow and how we speak as well). In general, this matches what musicologists have said of folk tunes of the past. For example, concerning Celtic melodies, Bradley suggested that 60% were ionian (major), 20% were mixolydian, 12% were aeolian (natural minor), and 8% were dorian.^[vi] Breathnach suggested 60% were ionian, 15% were mixolydian, 10% were dorian, and aeolian tunes were the least numerous.^[vii]

I have found similar results. While I was taking a break from the University of Otago and living in a Gaelic-speaking region of North America, I was approached by a publisher and asked to re-set The Celtic Lyre,^[viii] a set of four music books from about 1885; he wanted me to bring them up to modern standards. I decided to place the melodies so that the natural scale was apparent if applicable. Of the sixty-eight tunes, sixty-six could be easily played on a shepherd’s trumpet (that’s 97%); the other two were known to have been created on the bagpipes. This turned into a monumental project, but I eventually finished it.^[ix] I found the tunes ended on the following notes with these percentages: C: 54%, G: 21%, D: 13%, A: 12%. This is roughly in-line with the ecclesiastical modal attribution percentage that Bradley and Breathnach had given to Celtic folk songs. If this is written as the percentages of The Celtic Lyre/Bradley/Breathnach, we have: ionian (54%/60%/60%), mixolydian (21%^[x]/20%/15%), aeolian (12%/12%/least numerous), and dorian (13%/8%/10%). That’s quite a coincidence considering that 97% of the tunes of The Celtic Lyre could easily be played on a shepherd’s trumpet. This implies that the tunes analysed by Bradley and Breathnach could also be played by shepherds’ trumpets.

If we match the natural scale to the ecclesiastical modes, we get in order of theoretical likelihood:^[xi] ionian (C₄, C₅, also G₄), aeolian (E₄, A₄), mixolydian (G₄), dorian (D₅).^[xii] This would suggest why “[T]he modes on A and C were excluded from the ecclesiastical list, their effect judged as being ‘lascivious’ and ‘worldly’ and unsuitable for religious use since their influence would be pernicious.”^[xiii] So if you assume that my theory is correct, everything makes sense. Pastoral melodies were played on shepherds’ trumpets that trained musicians would describe as being the equivalent to the ionian and aeolian (and some mixolydian and some dorian) modes. The church banned those modes and pastoral instruments from church because they were linked to coarse, immoral behaviour. Over time, the forbidden modes became increasingly acceptable until they overwhelmed the ecclesiastical modes.^[xiv] By that time, the culture and the instruments that created that fulcrum of change had all but disappeared.^[xv]  

I should also point out that although my Ph.D. thesis is focused on medieval Gaelic narrative song, barriers placed between cultures, such as between Gaels and Saxons, are often created by modern nationalistic notions. Shepherds’ trumpets were spread all over Europe; folk music from various cultures, including those of the English, Welsh, Irish, Scottish, French, German, Italian, Spanish, and others, exhibit the same pitch-traits and have been described in the same way and with the same ending-note percentages as I found in The Celtic Lyre. The various languages represented by the names of shepherds’ trumpets listed above testify to their widespread use throughout Europe.

You may not believe me, but try to find the natural scale in old folk tunes for yourself. I gave directions on how to do this in The Celtic Lyre^[xvi] and online,^[xvii] but here it is in a nutshell: transpose the tune so that there are no accidentals in the key signature. Transpose the tune up or down a fourth or fifth (this doesn’t change the key signature in pentatonic tunes) so that the “missing” notes are on F₄ and B₄ or B₄ and F₅. For hexatonic tunes, place the “missing” note on B₄. Transpose the tune up and down until you see the lower pitches lock in to the natural scale. If this process doesn’t work, check the tune’s provenance. Often, tunes were composed on a piano to mimic older songs. The composers made the songs pentatonic, but didn’t gap them in the lower octave; for example, D₄ might fall on a stressed beat, and you can’t transpose it away.^[xviii]

While this theory is a simple solution to a long-standing problem, a deeper issue is how we as ethnomusicologists approach the music of other cultures. We have the diatonic scale driven into our bones by our schooling; therefore, we have a propensity to unconsciously direct this on the cultures that we are studying with the greatest sincerity and the best of intentions. Unfortunately, there are unseen, hidden tendencies that are a part of our everyday thoughts and behaviours that cause us to make choices that can have destructive results. The diatonic scale is one of them. Be on guard.

Click here for a full explanation of this theory with many examples

Click here for a video of this tradition as it is alive today